Research Labworks for MSc
The Research Labwork in Physics in the 1. and 2. master semester serves the purpose of training in a specific physical issue as well as project planning in order to improve experimental skills.
One project should be completed during the semester at one afternoon per week (4 CP). The experiments can be chosen from one of the following topics: optics, solid state physics, astronomy, computational physics, and material science. Depending on the specific conditions, one project can be done by either on or more students, in the latter case, with complementary tasks.
Students who would like to take the Research Labwork in the winter semester 2025/26 please register immediately with the advanced lab course office or in Friedolin. The registration for the respective projects in the moodle list in this summer semester will start Wednesday, October 1th, 2025 at 10 am.
At the end of the winter semester (25th of January, 2026) students will submit their results in form of a scientific poster. The presentation of the poster will be on 4th of February, 2026 at the F-Praktikum (attendance is mandatory).
The Organization of the research labwork is managed by the F-Praktikum office. If there are any questions, please contact us via physik.f-praktikum@uni-jena.de. Please do not send requests individually to project supervisors.
Laserphysics/Optics
-
Advanced Experimental Microscopy - Super-Resolution Microscopy
Seeing is believing. This sentence is as true as it is tricky. Most cellular components and processes, crucial for the nuanced understanding of (human) life, are not observable by conventional light microscopy since Abbe’s Law describes their maximum resolution to roughly half the wavelength of the observed light. This law is literally set in stone in Jena. However, over the past 15 years several ways of cleverly circumventing this diffraction limit were developed and implemented, achieving three-dimensional resolutions down to the nanometer range, resulting in the ever-growing field of optical super-resolution microscopy, for which the 2014 Nobel Prize in Chemistry was awarded.
The aim of this projects is to introduce, understand and apply the principles of state of the art fluorescence microscopy techniques, used e.g. in a broad range of modern biomedical and cell-biological research. Students prepare their own, fluorescently labeled, biological samples and will image them on a variety of advanced microscopes with different (resolution) capabilities. The qualitative and quantitative comparison of acquired images will illustrate the advantages and limitations of the respective microscopy technique.
Goals and Context
- Principles and application of advanced fluorescence microscopy techniques
- Concept of diffraction-limited and super-resolution
- Preparation of fluorescently labeled, biological samples
- 3D & multi-colour imaging at the nanoscale
Methods
- Cell culture and wet lab
- Fluorescent labeling
- A selection of advanced fluorescence microscopy techniques from the IAOB toolbox:
- Confocal Laser Scanning Microscopy
- Array Scan Microscopy
- Stimulated Emission Depletion (STED)
- Structured Illumination Microscopy (SIM)
- Single-Molecule Localization Microscopy (SMLM)
- MINFLUX Nanoscopy
- Image analysis by Fiji/ImageJ
Prerequisites
- An open mind and motivation for independent thinking
- Students should be able to explain the general difference between confocal and widefield microscopy and have basic knowledge on the concepts of super-resolution microscopy (e.g. Abbe’s diffraction limit)
- You should know the basic principles of fluorescence
A good preparation for the course is the biophysics lecture from Prof. C. Eggeling
Person in charge: Christian Franke & Katharina Reglinski
Supervisors: Christian Franke & Katharina Reglinski
Venue: Microscopy Labs of the IOAB in the ZAF and Abbeanum or at the IPHT (Beutenberg)
The topic is suitable for two groups with 1-2 students each.
-
Femtosecond Laser
Nowadays the generation of ultra-short laser pulses with a duration down to some femto seconds is state of the art. Such pulses find their application not only in the field of scientific research to investigate ultra-fast processes, to perform ultra-precise spectroscopy, or to generate extreme electrical and magnetic fields through ultra-high light intensities, but they are also applied in material processing, medicine, especially in ophthalmology. Nevertheless, the generation and metrology of ultra-short pulses require complex measurement techniques. The basics to understand the underlying effects of pulse generation, stretching and compression as well as their measurement will be taught here. Some of these effects are based on non-linear optics and frequency conversion, that requires phase matching to get reasonable efficiencies. Second harmonic generation and two-photon absorption are used for pulse characterization by auto-correlation here. The limitations of the auto-correlation for the reconstruction of the temporal behavior of the laser field will be investigated in more detail.
Teaching goals and content
- Working principle and properties of solid-state lasers (Ti:sapphire)
- Cavity stability and longitudinal cavity modes
- Dependence of output power on pump power
- Generation of femtosecond pulses by Kerr-lens mode-locking
- Compensation of group velocity dispersion in optical cavities
- Impact of spectral phase on pulse duration and temporal pulse shape
- Measurement of band-width and duration of laser pulses
- Application of Fourier-Transform to explain pulse stretching and compression
- Interferometric and intensity auto-correlation and their limitations for pulse characterization
- Measurement of group velocity dispersion (GVD) of several materials
Experimental techniques and equipment
- diode-pumped, frequency-doubled 5W Nd:YV04-laser as pump source
- homemade Ti:sapphire femtosecond laser with prism GVD compensation
- external prism pulse compressor
- optical spectrometer
- second harmonic generating auto-correlator
- photodiodes, powermeter and oscilloscope
Contact:
Supervisor: Dr. Joachim Hein
Place: F-Praktikum
For this experiment two students are recommended.
-
Femtosecond pulse chirp estimation
Ultrashort laser pulses have a large spectral width. These pulses acquire a certain amount of chirp (modulation of the spectral phase) and thus change their temporal shape when propagating in a material with dispersion. Measuring the pulse spectrum is not sufficient to estimate the pulse width and shape because it does not contain information about the spectral phase of the pulse. Although there are some sophisticated measurement techniques available to reveal this, a simpler approach is pursued here: the extraction of spectral phase information from a second order interferometric autocorrelation. Such an autocorrelator is used to measure the pulse width of a home-built femtosecond Ti:sapphire laser. When the pulses contain a significant amount of chirp, pulse width estimation is not as simple as extracting it from the width of the autocorrelation trace. The goal of this project is to write a program, e.g. in Phython, Julia or any other programming language, to compute the higher order chirp coefficients from the measured spectrum and the interferometric autocorrelation trace. This code could be used to automate the temporal pulse characterization.
Teaching goals and content
- Working principle of second harmonic autocorrelation
- Behavior of femtosecond pulses with chirp
- Application of programming tools for data evaluation
- Programming with open source software
Experimental techniques and equipment
- homemade Ti:sapphire femtosecond laser with prism GVD compensation
- optical spectrometer
- second harmonic generating auto-correlator
- photodiodes, powermeter and oscilloscope
Contact:
Supervisor: Dr. J. Hein
Place: F-Praktikum
For this computational project one student is recommended, but two are possible as well.
-
High efficiency pulse self-compression and mode cleaning in periodic nonlinear Media
The quest to generate as short as possible coherent optical pulses started simultaneously with birth of laser physics. Ultrashort laser pulses have critical importance for time-resolved linear and nonlinear spectroscopy, achieving extreme peak values of electric field strength for physics of strong field light-matter interaction etc. Numerous methods were developed that enable today laser pulses with duration down to single optical cycle. At low energy/peak power level (roughly below 1 µJ for modern femtosecond laser sources), methods based on nonlinear spectral broadening with subsequent linear dispersion management, or solitonic self-compression in conventional or photonic crystal structure optical fibers are used. For high (multi-mJ) energy laser pulses, spectral broadening in gas-filled hollow-core fibers or filamentation in gases is used to achieve temporal compression down to single cycle.
The goal of the proposed project is experimental realization and optimization of a novel pulse self-compression technique suitable for femtosecond laser pulses with energy 1-100 µJ. This technique is based on complex spatial and temporal dynamics of intense, ultrashort laser pulses in periodic nonlinear media with cubic (Kerr) nonlinearity. The advantage of this technique is that it is very robust (essentially alignment free), has very high (close to 100%) efficiency in terms of energy content in the compressed pulse relative to the initial pulse energy, enables additionally excellent spatial distribution of intensity due to nonlinear mode cleaning and can be applied to laser pulses with wavelengths from UV to mid-IR spectral range.
Prerequisites:
- Basics knowledge in optics
- Good experimental skills
Supervisor: Dr. Daniil Kartashov
Place: Institute of Optics and Quantum Electronics (IOQ, Max-Wien-Platz 1)
The topic is suitable for one or two students.
-
High Resolution Computational Imaging – Ptychography
Ptychography is an advanced computational imaging technique used in electron, X-ray, EUV, and visible-light microscopy to achieve high-resolution images beyond the limits of conventional lenses. It is a form of coherent diffraction imaging (CDI) that reconstructs an object's structure by analysing diffraction patterns from multiple overlapping illumination positions. In particular, it enables quantitative imaging of the sample’s transmission function in both amplitude and phase, providing access to the local density, local material composition, and local thickness of complex structures.
The aim of this project is to apply the ptychography technique to imaging of vaious biological samples and understand is principles and advantages. You will particularly investigate the influence of different scan grids and illumination beams on the image quality and resolution.
Teaching goals and content
- Understand the basics of ptychography
- Perform systematic ptychography measurements on various samples
- Apply the pty:lab toolbox to reconstruct Ptychography datasets
- Explore the influence of the scan grid and different illumination beams on image quality and resolution
Experimental techniques and equipment
- Visible ligth ptychography setup
- Pty:Lab computational toolbox (https://github.com/PtyLabExterner Link)
- Different laser sources
- Scientific CMOS detectors
Prerequisites
- Interest in computational imaging
- Basics knowledge in Optics and Fourier-Optics
- Basic programming skills in Python or Matlab
- Experimental skills (optical setups) and problem-solving ability
Contact:
Supervisor: Jan Rothhardt and Cesar Jauregui
Place: Institute of Applied Physics, Abbe-Center-of-Phtonics (Beutenberg)
The topic is suitable for one or two students.
-
Imaging without imaging: using algorithms to replace optics
In modern optical imaging, precise methods for investigating micro- and nanoscale structures are of great importance. Diffraction imaging revolutionizes optical imaging by foregoing traditional optics and instead relying on computer algorithms to create high-resolution images. Despite its potential, there are significant challenges in reconstructing images from diffraction patterns.
The main focus of this project is to investigate the optical diffraction imaging in the visible range. The various influences such as the size of the illumination spot, the coherence, the structure size, the monochromaticity or bandwidth and the overlap with other beams in the visible spectral range will be taken into account. A particular focus will be on exploring the convergence of reconstruction algorithms as a function of the above parameters. In particular, multicolor diffraction still raises many fundamental questions.
Teaching Goals and Content
- Design and construction of an optical test setup
- Basics of diffraction imaging and ptychography
- Influence of various light sources on imaging
- Development and application of reconstruction algorithms
- Experimental applications and diagnostic methods
Prerequisites
- Basics in optics, Fourier optics, and image processing
- Interest in modern imaging and algorithm development
- Experimental skill and problem-solving ability
- Basic knowledge in programming, ideally in Python or Matlab
Contact:
Supervisor: Dr. Martin Wünsche and Dr. Jan Rothhardt
Place: Max-Wien-Platz 1 and Albert-Einstein-Str. 6
The topic is suitable for two groups with 2 students each.
-
Measuring the optical beam generated by flat-optics photonic devices
Flat photonics have emerged in the last few years as a disruptive technology for the manipulation of optical wavefronts. The big advantages of flat photonics are the compactness and the absence of aberration due to curved interfaces, an inherent limit in standard lenses. The concept is based upon the transverse structuring of the material, inducing a local phase delay independent from the thickness. By changing the phase across the beam cross-section, the optical propagation can be sculpted at will, going well beyond the functionality of standard lenses.
The goal here is to characterize photonic devices in glass obtained by structuring locally the material with intense pulsed beams. The large intensity of the writing beam makes the glass locally anisotropic. The control on the local anisotropy permits to control the phase delay (i.e., the optical path), allowing to write a phase hologram featuring a large degree of tunability.
The main aim of the work is to fully characterize the optical propagation after the device. To accomplish the goal, an automatized characterization set-up capable of measuring the beam profile at different distances is required. The work will include writing a Python code capable of moving a translation stage and integrate this library with the currently available software controlling an in-house made polarimeter. Once the setup is ready, the candidate will characterize beam deflectors, lenses and gratings based upon flat optics.
Teaching goals and content
- Wavefront manipulation via holograms
- Measurement automatization based on Python
- Integration between different systems
- Acquiring hands-on expertise in estimating the accuracy of a measurement
- Learning how an imaging system works
Prerequisites
- Fundamental optics, especially Gaussian beams and diffraction
- Confidence with lab work
- Basic knowledge of Python
- Interest in photonics and modern optics
Supervisor: Dr. Jisha Chandroth Pannian / Dr. Alessandro Alberucci
Place: Institute of Applied Physics (IAP, Beutenberg)
-
Ultrafast fiber laser oscillators
Ultrashort pulse lasers are nowadays one of the most interesting types of lasers, since they have opened up new applications in the scientific, medical and industrial fields. In fact, achieving ultrashort pulses (<1ps) is a unique ability of lasers that separate them from other light sources. Usually such ultrashort pulses, which are some of the shortest events ever created by Mankind, are obtained using the technique of mode locking, which has become one of the most important methods in modern lasers.
Additionally, among all available laser architectures, fiber lasers have stablished themselves as one of the most attractive types of lasers due to their simplicity, efficiency, low-cost, maintenance-free nature, compactness, robustness and high-power scalability. In fact, fiber lasers are currently replacing more traditional types of lasers in many applications.
In this project, you will get to know fiber lasers by building and characterizing a mode-locked fiber laser able to deliver several 100 fs pulses. In this project you will build the cavity, try out different configurations and learn about the physics of mode locking. At the end, you will have created from scratch one of the most appealing types of lasers: an ultrafast fiber laser.
Teaching Goals and Content
- Understand the principles of mode-locking and fiber lasers.
- Design and construct a fiber cavity.
- Use of Semiconductor-Saturable Absorber Mirrors (SESAMs) to achieve mode-locking.
- Learn to characterize an ultrafast laser.
- Analyze the performance of the laser as different parameters of the cavity are changed.
- Perform simulations of the laser.
Experimental Techniques and Equipment
- Handling of optical fibers (stripping, cleaving, splicing, etc).
- Coupling of optical radiation in/out of a fiber.
- Use of SESAMs.
- Systematic characterization of the laser performance using, e.g. power meters, spectrometers, etc.
Contact:
Supervisor: Cesar Jauregui & Jan Rothhardt
Place: Institute of Applied Physics/Abbe center of Photonics
This experiment can be carried out by one of two students.
Solid State Physics
-
Entwicklung eines Oberstufen-Experiments zur Lithographie
Nanostrukturen prägen unseren Alltag im 21. Jahrhundert: Sie stecken in nahezu allen elektronischen Geräten, treiben die zweite Quantenrevolution voran und gelten als Schlüsseltechnologie für zukünftige Energiesysteme – bis hin zur Kernfusion. Gerade weil Nanotechnologie so grundlegend ist, sollte ihr Verständnis bereits in der Schule beginnen.
Dieses Praktikumsprojekt schlägt eine Brücke zwischen aktueller Forschung und Unterrichtspraxis: Mit einfachen, kostengünstigen Komponenten wird ein anschauliches Schülerexperiment entwickelt, das zentrale Prinzipien der Lithographie greifbar macht – reproduzierbar, sicher und didaktisch durchdacht.
Zielsetzung
Entwicklung eines leicht nachbaubaren Aufbaus zur Proximity-Lithographie für den Einsatz in der gymnasialen Oberstufe. Der Aufbau soll überwiegend aus 3D-gedruckten Komponenten und gängiger Konsumelektronik bestehen, sodass Schulen ihn mit vertretbarem Aufwand übernehmen können.
Aufgaben / Lernziele
- Verständnis der Grundprinzipien der Lithographie und ihrer Anwendungen.
- Entwurf und Aufbau eines funktionsfähigen Prototyps für ein Oberstufen-Experiment.
- Durchführung ausgewählter Arbeitsschritte in einem professionellen Reinraum (nach Einweisung).
- Ausarbeitung eines Posters zur Präsentation des Aufbaus (Zielgruppe: Lehrkräfte/Schüler*innen).
Voraussetzungen
- 3D-Design und erste Erfahrung im 3D-Druck
- Grundkenntnisse im Programmieren
- Interesse an Experimentdesign und naturwissenschaftlicher Didaktik
- Gute Kenntnisse der deutschen Sprache
- Programmiersprachen (nach Bedarf): Python, C, C++
Betreuer: Dr. Thomas Siefke
Das Projekt kann von 1 oder 2 Studierenden durchgeführt werden.
-
Hands-On Optical Characterization with a Transmittance/Reflectance Setup
Transmittance/reflectance spectroscopy is a simple linear optical method to find absorption lines of materials. Typically, a white light source, which spans a large wavelength range illuminates the sample. Then, either the light transmitted through (transmittance) or reflected on (reflectance) the sample is compared to a reference, where the light is transmitted through/reflected on the substrate. Finally, the light is detected wavelength-resolved in a spectrometer.
While this is a very common setup, used to characterize all sorts of materials, this setup is meant to analyze two-dimensional materials within our research group. Because of the ultra-low thickness of two-dimensional materials (below 1 nm), they interact weakly with light, absorbing less than 1% of the light. Therefore, a high sensitivity and stability of the setup is crucial.
In this project, we will design, build and test such a transmittance/reflectance setup. The goal of this experiment is to enable students to understand basic concepts of how to build simple optical setups and characterize their performance.
During the first weeks we will start discussing the measurement method in detail and plan the setup schematically. In the following weeks, the setup shall be built by the students, before finally testing the setup capabilities on several two-dimensional materials like graphene, transition metal dichalcogenides etc., which are regularly studied within our research group.
Working plan:
Weeks 1 -4: Introduction to linear optics and transmittance/reflectance spectroscopy, schematic design of the optical setup
Weeks 5-8: Building the transmittance/reflectance setup
Weeks 9-12: testing and characterizing the assembled setup on several two-dimensional materials
Objectives
- Enable students to design and build simple optical setups
- Apply transmittance/reflectance spectroscopy to two-dimensional materials
Experimental techniques
- Linear optics: transmittance/reflectance spectroscopy
- Basic linear microscopy
Supervisor: Paul Herrmann (Vipin Krishna)
Venue: GUFOS, IFK (Room E011)
The topic can be worked on by one or two students. Supervision is possible in English and German.
-
In-situ Flux Measurement in a Broad Ion Source
Ion sources are applied in a wide range of processes for e.g. doping, quantum dot fabrication and the creation of buried layers. For theses purposes, broad beam ion sources can be utilized to maintain fast processing times even on large implantation areas.
In 2022, operation of a unique four-grid accelerator broad ion source (4GABIS) started at the IAP Jena. Within 4GABIS, ions are accelerated from a plasma source with voltages of up to 30 kV in a beam of around 180 mm diameter. Currently, 4GABIS is not completely characterized for all of the available acceleration parameters. Hence, the first goal of the experiments is to investigate the effect of grid voltages on the resulting shape of the beam profile. This will be measured both directly with a movable faraday cup and indirectly via resulting sputter rates. The insights of this will subsequently be applied to establish ratios between the flux of ions hitting the target and the faraday cup in measurement position, respectively. Next to that, the impact of neutralisation of ions during their flight via charge transfer will be measured. From this, charge transfer cross sections can be calculated and compared with the literature. The combined results are to be integrated into a pre-existing LabVIEW program to allow for in-situ measurement of ion flux.
Summary of the main goals for this experiment:
- Understanding the shaping of a hot-cathode glow discharge plasma
- Investigation of grid voltage parameters to affect the resulting ion beam
- Measurement of charge transfer cross section for collisions of ions and residual gas
- Combining parameters necessary for in-situ monitoring of ion flux
Prerequisites:
- Basic understanding of hot cathode glow discharge and ion acceleration
- Basic knowledge of LabVIEW programming
- Good laboratory skills
- Interest in operating a unique ion source
Contact:
Supervisor: Johannes Kaufmann
Venue: Institute of Applied Physics, Beutenberg Campus (Albert-Einstein-Str. 15)
The topic is suitable for one or two students.
-
Investigation of Multilayer Mirrors for X-Rays
Learning target and topics
- Thin metal layers: deposition, characterization of the layer properties and structure
- High vacuum technology
- Introduction and application of various analysis methods
- Scanning Electron Microscopy (SEM) and Energy Dispersive X-Ray Analysis (EDX)
- Scanning Tunneling or Atomic Force Microscopy (STM, AFM)
- AugerElectronSpectroscopy (AES)
- X-ray diffractometry
Experimental equipment
- Sputter coating system from Oxford Instruments
- Thermal evaporation system (self-made)
- Mass Spectrometer for residual gas analysis
- Scanning Electron Microscope
- Atomic Force Microscope
- Scanning Tunneling Microscope
- Auger Electron Spectrometer
Supervisor: MSc. Markus Walther & Dr. Thomas Siefke
Venue: F-Praktikum, IFK and IOQ
The topic is suitable for one or two students.
-
Low-Cost Single Crystalline Metal Layers: Fabrication and Characterization
Single crystalline metal layers on natural mica are often used in electronic devices such as transistors, solar cells, and sensors, due to their high electrical conductivity and mechanical stability. Additionally, they can be used as a substrate for growing other single crystalline materials, such as semiconductors, which can be used in electronic devices as well. The high thermal and chemical stability of natural mica also makes it an ideal substrate for a wide range of applications, such as in the aerospace and automotive industries. Overall, the cost-effective fabrication of single crystalline metal layers on natural mica can have a significant impact on the development of new technologies and the improvement of existing ones.
The experiment aims to fabricate and investigate the properties of single crystalline metal layers using a thermal evaporation method. In this process, the metal material will be thermally evaporated onto a substrate of natural mica under specific conditions, such as temperature, pressure, and evaporation rate, to achieve single crystalline growth. The substrate will be carefully chosen, cleaned and prepared to ensure optimal growth conditions.
The characterization of the fabricated metal layers will be done using a combination of techniques including atomic force microscopy (AFM) and x-ray diffraction studies (XRD). The AFM will be used to observe the surface morphology of the metal layers, including the thickness, uniformity, and surface roughness. The XRD will be used to determine the crystal structure of the metal layers, including the crystal size, lattice spacing, and crystal orientation, as well as to identify any defects or impurities in the crystal structure.
The goal of the experiment is to understand how the thermal evaporation fabrication method and process conditions affect the properties of single crystalline metal layers and how such layers can be used in various applications such as electronics, catalysis, and sensing. The experiment will also help in understanding the relationship between the growth conditions and the crystal structure and will provide a better understanding of the fundamental physics of metal growth.
The main goals of this experiment are:
- Fabrication of single crystalline metal layers using thermal evaporation
- Investigation of the structural and morphological properties
Prerequisites:
- Familiarity with basic laboratory techniques
- Basic understanding of crystal growth and crystal structure
Methods:
- Thermal evaporation setup
- Atomic force microscopy (AFM)
- X-ray diffraction studies (XRD)
Contact:
Supervisor: Dr. Marco Grünewald
Language: German or English
Venue: F-Praktikum and labs of the IOQ
The topic is suitable for one or two students.
-
NanoFabLab
Micro- and nanotechnology forms the basis for a growing number of everyday objects and current scientific research. Many physical systems require a direct examination or at least a basic understanding of this technology chain.
The theoretical foundations are already taught at the FSU as part of the Micro/Nanotechnology lecture in the Physics or Photonics Master's programme and the associated seminar. Practical training has not yet been provided. This gap is to be closed by expanding the programme of the lab course.
The aim of this offer is to gain initial experience with an existing lithography line in the clean room and to jointly develop a concept for how this can be used for future teaching.
Contact:
Supervisor: MSc. Nishitha Prabhakaran & Dr. Thomas Siefke
Venue: Clean room of the IFK and F-Praktikum
The topic is suitable for one or two students.
-
Nonlinear Optics in Trilayer Graphene: Probing Stacking Order via Second Harmonic Generation
Nonlinear optics is a cornerstone of modern science and technology, enabling frequency conversion, spectroscopy, sensing, and ultrafast light control. Two-dimensional (2D) materials offer exceptional opportunities in this field due to their strong optical response, atomic thickness, and ease of integration into photonic platforms.
In this lab project, we will investigate how nonlinear optics can be used to probe stacking order in trilayer graphene, focusing specifically on the difference between ABA (Bernal) and ABC (rhombohedral) stacking. Using second harmonic generation (SHG), we will demonstrate how inversion symmetry present in ABA but absent in ABC, leads to fundamentally different second-harmonic (SH) responses (Shan et al. Sci. Adv. 4, eaat0074, 2018).
The students will begin by exfoliating trilayer graphene flakes and using Raman spectroscopy to distinguish between ABA and ABC domains based on their characteristic 2D-mode signatures. After identifying and statistically analyzing stacking types, we will perform power-dependent SHG measurements on each domain type to confirm that SHG is only present in non-centrosymmetric (ABC) regions under low excitation conditions while SH signal starts to appear for higher excitation fluences in centrosymmetric (ABA) trilayer.
This project introduces concepts of nonlinear optics and symmetry breaking, and provides hands-on experience with optical microscopy, Raman spectroscopy, polarization optics, and SHG detection.
Working plan:
Weeks 1–4:
- Introduction to nonlinear optics in 2D materials, symmetry considerations.
- Exfoliation of trilayer graphene on SiO2 substrates.
- Raman spectroscopy for ABA vs ABC domain identification.
Weeks 5–8:
- Calibration and alignment of SHG setup.
- Power-dependent SHG measurements on ABA and ABC trilayers.
- Statistical mapping and analysis of stacking-sensitive SHG response.
Weeks 9–12:
- Polarization-resolved SHG (confirming symmetry behavior).
- fs laser exposure for domain manipulation and SHG contrast changes.
- Final presentation and discussion.
Objectives
- Understand nonlinear optical processes (SHG) in 2D materials.
- Learn to distinguish stacking order using Raman and SHG.
- Study how inversion symmetry affects nonlinear light–matter interaction.
- Gain experience with polarization optics and spatially resolved spectroscopy.
Experimental techniques
- Raman spectroscopy and domain analysis
- SHG microscopy
- Power-dependent and polarization-resolved SHG
- Optical microscopy and exfoliation techniques
Supervisor: MSc. Omid Ghaebi
Venue: GUFOS, IFK (Room E002)
The topic can be worked on by one or two students. Supervision is only possible in English.
-
Photoelectron Diffraction of Crystalline Surfaces
According to de Broglie matter has not only particle but also wave character. It was shown that electrons, due to their rest mass, already exhibit wavelengths of around 1 angstrom at acceleration voltages of about 150 V, which is in the range of atomic distances in solids. Crystals therefore represent natural diffraction gratings for accelerated electrons, just as they do for X-rays of similar wavelengths. However, due to the strong inelastic interaction between electrons and atoms, the inelastic mean free path of electrons in solids ranges from less than 1 to several 100 nm which is thus considerably smaller than for X-rays. This makes electron diffraction especially suited for the investigation of crystalline surfaces and thin layers.
The aim of this projects is to understand principles of a special type of electron diffraction, namely X-ray photoelectron diffraction (XPD). This method enables an element specific analysis of the structure of a crystalline surface. For comparison, low-energy electron diffraction (LEED) will also be performed as a widely used characterization method for inorganic compounds. Students will learn how to prepare their own samples, starting from cleaning single-crystal surfaces, followed by the deposition of films via molecular beam epitaxy as well as their structural characterization by means of LEED and XPD. All preparation and analyzing steps are performed under ultrahigh vacuum (UHV) conditions.
Goals and context
- principles and application of electron diffraction in two dimensions (2D)
- concept of reciprocal space
- preparation of atomically clean single crystals and two dimensional materials
- highly-ordered ultrathin layers by molecular beam epitaxy
- vacuum technology (pumps, gauges, rest gas analysis etc.)
Methods
- UHV chambers with:
- Photoelectron spectroscopy setup (X-ray source, hemispherical analyzer)
- MCP-LEED (electron gun, phosphor screen, micro channel plates, camera)
- sputter gun and sample heater
- vacuum pumps (roughing, turbo, ion getter, and titanium pump)
- metal single crystals as sample substrates
Contact:
Supervisor: MSc. Maximilian Schaal & Dr. Felix Otto
Venue: Labs of AG Fritz (ZAF)
The topic is suitable for two students.
-
Vacuum Coating of Thin Metal Layers
Thin layers are layers with thicknesses in the micrometer and nanometer range. Their physical parameters such as electrical conductivity often deviates from that of the bulk material, allowing for altered, tailored properties and new functionalities. In addition, the material savings are often of great economic importance. Well known is the application in the field of protection against environmental conditions, e.g. against corrosion or oxidation. However, thin layers are most important in microelectronics, where almost all components are manufactured using thin-film technology. In optics, thin layers and layer stacks are used to influence the reflection and transmission behavior, but also the polarization. In particular, layer systems play a prominent role in X-ray optics.
In the internship, metallic layers are usually deposited and characterized by different methods. Concrete topics and goals, amongst others taken from current research projects, are proposed by the supervisor at the beginning of the internship, but can be discussed and adapted depending on the interests.
Learning goals and content:
- Deposition of thin metal layers by means of various coating methods (sputter coating, thermal evaporation)
- Characterization of the layer properties (e.g., composition, roughness, crystalline properties) depending on substrate properties and coating parameters (e.g. chamber pressure, residual gas composition, process times, substrate heating)
- Introduction and application of various analysis methods
- Scanning Electron Microscopy (SEM) and Energy Dispersive X-Ray Analysis (EDX)
- Scanning Tunneling or Atomic Force Microscopy (STM, AFM)
- Auger Electron Spectroscopy (AES)
- X-ray diffractometry (in cooperation with the X-ray group)
Experimental equipment:
- Sputter coating system from Oxford Instruments
- Thermal evaporation system (self-made)
- Mass Spectrometer for residual gas analysis
- Quartz layerthickness monitor
- Scanning Electron Microscope
- Atomic Force Microscope
- Scanning Tunneling Microscope
- Auger Electron Spectrometer
Contact:
Supervisor: MSc. Markus Walther & Dr. Thomas Siefke
Venue: F-Praktikum
The topic is suitable for one or two students.
Computational Physics and Theory
-
A density-matrix approach to atomic photoionization
In quantum mechanics, the “density matrix” is an alternative and often more complete concept (than the well-known wave function) in order to describe the quantum state of a physical system. It enables one to compute quantum probabilities for the outcome of measurements, if the quantum system is in a mixed state. The density matrix is particularly useful, if the initial state of the system is not fully known or if it interacts and becomes entangled with some environment. Density matrices have therefore been found crucial in many research areas, such as atomic and molecular physics, quantum information or the study of decoherence.
In this project, we wish to apply the (atomic) density matrix theory to study the photo-ionization of simple, i.e. hydrogenic and few-electron, atoms. The density matrix is appropriate here, if we need to analyze the angular distribution or spin polarization of the emitted electron, and if the photo-ion remains unobserved. The great advantage of atomic density matrices are that they can readily be limited to the physical states of interest and, hence, are still rather low-dimensional.
Goals of the project
- Recall the treatment of quantum systems in terms of wave functions and density matrices.
- Explore the SO3 rotational symmetry of atoms and ions
- Describe the interaction of atoms with a weak radiation field
- Develop a program for the setup of small density matrices and their analysis for possible observables
- Optional: Describe the interaction of atoms and molecules in terms of a multipole expansion of the radiation field (spherical tensors)
Prerequisites:
- basic knowledge of quantum mechanics
- programming skills (Python, Julia, C)
Contact:
Supervision: Prof. Stephan Fritzsche, Theoretisch-Physikalisches Institut
Where: Theoretisch-Physikalisches Institut & Helmholtz-Institut Jena, Frauenhoferstr. 8.
Per term, one or two students may work on the project
-
Atomistic Quantum-Mechanical Simulations of Low-Dimensional Materials
Goals and context
This lab project provides a comprehensive introduction to atomistic quantum-mechanical simulations, specifically utilizing density-functional theory (DFT), for investigating the properties of nanomaterials. DFT enables parameter-free simulations and analysis of material characteristics, offering a powerful complement to experiments.
In recent years, low-dimensional semiconductors, such as transition metal dichalcogenide monolayers, have garnered significant attention due to their exceptional optical properties and potential for next-generation optoelectronic applications. Their mechanical flexibility further allows for the creation of van der Waals heterostructures by combining single layers of the same or different materials. This versatility opens up a vast landscape of novel materials with tunable characteristics that can be efficiently disclosed from first principles.
This project will provide basic knowledge and practical skills to conduct ab initio simulations on low-dimensional materials using DFT. Key tasks include structure optimization, calculations of electronic properties (including quantum effects), and comparison against available experimental data. Beyond running calculations, basic programming skills (preferentially in Python) will be trained to prepare or customize post-processing and visualization scripts.
The specific research focus will be tailored to align with the interests of the participating students, ensuring an engaging and personalized learning experience.
Methods
- Density functional theory
Prerequisites
- Knowledge of quantum mechanics and elements of programming are requested
- Knowledge of solid-state theory and Python are an asset.
Organization
Person in charge: Prof. Dr. Caterina Cocchi
Supervisor: Dr. M. Sufyan Ramzan, Prof. Dr. Caterina Cocchi
Place: IFTO, Abbeanum
-
Computer experiment: Simple quantum error correction protocols
Quantum error correction (QEC) aims to protect fragile quantum information from being affected by decoherence and (various) unwanted interactions with the environment. Unlike to the use of classical bits, however, qubits can neither be copied nor corrected by just introducing a parity bit. Instead, some redundancy and entanglement of physical qubits need to be utilized in order to encode information in such a way, that their errors can be detected and corrected without destroying the quantum state of the associated logical qubit. QEC currently receives much attention because reliable error correction is essential for building scalable, fault-tolerant quan-tum computers.
Modeling simple QEC protocols is possible also on classical computers by simulating qubits, gates, and noise processes using classical algorithms. While these classical simulations cannot be scaled to large quantum systems, they enable us to understand, test and analyze error correction codes on small numbers of qubits.
This project aims to understand and to implement simple QEC protocols (for instance, Steane’s 5-qubit code). We also wish to explore the effectiveness of these protocols and how they might guide experimental implementations in the future.
Goals of the project
- Recall and understand a few simple QEC protocols for protecting logical qubits with regard to different types of noises
- Encode the logical information into physical qubits in such a way that noise errors can be detected
- Work with the (generalized) Pauli matrices and the correlation tensor of few-qubit systems
- Design a program code for the correcting logical quantum registers if different noises occur with certain probabilities
- Explore and determine the effort for correcting logical n-qubit registers
- Optional extensions: How can noise be classified in terms of (so-called) quantum operations and Kraus’ operators
Prerequisites:
- basic knowledge of quantum mechanics
- programming skills (Python, Julia)
Contact:
Supervision: Prof. Stephan Fritzsche, Theoretisch-Physikalisches Institut
Where: Theoretisch-Physikalisches Institut & Helmholtz-Institut Jena, Frauenhoferstr. 8.
Per term, one or two students may work on the project
-
Dynamical and Thermal Stability of Semiconductors
Goals and context
This lab project is aimed at familiarizing the students with quantum-mechanical, atomistic computational tools to investigate thermodynamic properties of bulk semiconductors. To address a technologically relevant scenario, we will focus on alkali antimonides, a class of materials that are currently used as photocathodes in particle accelerator facilities, such as BESSY II in Berlin.
Calculations will be performed using density-functional theory (DFT), an established first-principles framework enabling the simulation of material properties without the need for empirical parameters. Key tasks of the project include structure optimization, to find the optimal lattice volume and minimize interatomic forces, and the calculation of phonon band structures and projected density of states to assess dynamic stability. Machine-learning–based methods will be employed to calculate force‑constant tensors more efficiently than traditional approaches. Beyond running calculations with established and widely used software packages, basic programming skills (preferentially in Python) will be trained to prepare or customize post-processing and visualization scripts.
The specific research focus will be tailored to align with the interests of the participating students, ensuring an engaging and personalized learning experience.
Methods
- Density functional Theory
- Machine learning
Prerequisites
- Knowledge of quantum mechanics and elements of programming are requested.
- Knowledge of solid-state theory and Python are an asset.
Organization
Person in charge: Prof. Dr. Caterina Cocchi
Supervisor: MSc. Julia Santana Andreo, Prof. Dr. Caterina Cocchi
Place: IFTO, Abbeanum
-
Modern Topics in Quantum and Gravitational Theories
Possible topics within this project are:
- Entanglement and its entropy measures in quantum mechanics
- Supersymmetric quantum mechanics
- Magnetic monopoles and quantization of electric charge
- Magnetic monopoles in theoretical condensed matter physics: From the Berry phase in quantum mechanics to the field theoretical description of Weyl semimetals
- Do particles exist interpolating between a fermionic and a bosonic behaviour? Anyons and their description in terms of Chern-Simons theory.
- Hawking radiation and evaporating quantum black holes*
*basic knowledge of general relativity and quantum field theory required.
Contact
Supervision: Prof. Dr. Martin Ammon
Venue: Theoretisch-Physikalisches Institut, Fröbelstieg 1 (Abbeanum)
One or two students may work on this topic per term.
-
Mathematica Research Labworks
Plot of point charges. Made in Mathematica.
Foto: Prof. Dr. BrügmannGoals and context
Computers have long been powerful tools for numerical computation, efficiently solving equations and simulating physical systems. Perhaps less well-known is the use of computers for non-numerical, symbolic calculations. Many areas of physics require complex analytic calculations – manipulating symbolic expressions for algebra or calculus. These tasks quickly become cumbersome and prone to errors when handled manually. Fortunately, we can leverage computers to assist with such challenges using software like Mathematica. Mathematica is a state-of-the-art computational tool offering sophisticated handling and manipulation of symbolic algebra, alongside powerful visualization capabilities that can be updated dynamically.In this project, students will use Mathematica to study the Lorentz transformation of Special Relativity, including boosts in arbitrary directions, the Thomas-Wigner rotation and Thomas precession. These are fundamental concepts in Special Relativity and appear in many branches of modern physics, from highenergy
theory in astrophysics to quantum mechanics. The calculations involve four-dimensional matrix algebra, which can be carried out by Mathematica, and the results can be visualised with Mathematica as well.Method
Students will learn general Mathematica skills applicable to many areas of physics and mathematics:
- Algebraic manipulation
- Visualisation of physical systems
- Symbolic computation
- Setting up Mathematica notebook
Prerequisites
- Basic knowledge of Special Relativity
- Basic knowledge of linear algebra
Contact
Person in charge: Prof. Dr. Bernd Brügmann
Supervision: Mads Sørensen
Venue: Abbeanum, Fröbelstieg 1 or PAF Computerpool
One or two students may work on this topic per term.
-
Navier Stokes Equation
Goals and context
Computational Fluid Dynamics (CFD) is a central part of computational physics and has been a driver for the development of modern numerical methods. It involves solving flow mechanical problems that cannot be solved analytically and are expensive to study experimentally by integrating generally nonlinear, partial differential equations.
In this project, the students will apply numerical methods to solve the Navier-Stokes-Equations for the case of an incompressible fluid to study flow within a cavity and flow around obstacles.
Methods
Timestepping schemes for integration of hyperbolic equations as well as a relaxation scheme for solving elliptic equations will be employed to solve the Navier-Stokes-Equations numerically on a staggered grid in two dimensions. The stability and convergence behavior of these schemes will be examinated.
The students will use C/C++, Python or Matlab to implement these methods.
Prerequisites
- Basic knowledge of partial differential equations
- Basic knowledge of numerical methods
- Familiarity with at least one of the suggested programming languages
Contact:
Person in charge: Prof. Dr. Bernd Brügmann
Supervision: Praveer Gollapudi
Place: Abbeanum, Fröbelstieg 1 or PAF Computerpool
Per term, one or two students may work on the topic
-
Rigorous Numerical Simulation of Quantum-Photonic Nanostructures
Goals and context
The strong coupling of light to quantum systems relies on the confinement of electromagnetic fields to sub-wavelength volumes. This can be achieved by hybrid nanophotonic quantum systems, in which photonic nanostructures support tightly confined electromagnetic resonances. Computer simulations are an essential part of this research since the fabrication of nanoscopic structures is challenging and the experimental characterization of optical fields at the few photon level with nanometer resolution is equally complicated. Therefore, reliable simulation methods are required to calculate the electromagnetic response of nanostructured matter in advance. Since we are dealing with structures in the sub-wavelength range, "rigorous" methods are needed, which solve Maxwell´s equations without any approximation. Different approaches have explored for certain classes of nanophotonic structures (micro and nano cavities, metasurfaces, nanoantennas).
Methods
The students will implement and use a rigorous numerical method (FDTD or FEM) for the solution of electrodynamic problems. They will either use one of the existing professional implementations of such methods or will be working on their own implementation in a programming language suitable for high-performance computing. The method will be used to simulate the behavior of a nanophotonic structure and to investigate the coupling to quantum systems.
Programming can be done in any language preferred by the students, but Python and Matlab are supported by existing implementations.
Prerequisites
- Basic knowledge of electrodynamics and related partial differential equations
- Basic knowledge of optics
- Basic knowledge of numerical methods
- Familiar with at least one programming language supporting numerical simulations (preferred Python or Matlab)
Contact:
Person in charge: Prof. Dr. Thomas Pertsch
Supervisor: Dr. Ángela Barreda
Place: Abbe Center of Photonics, Campus Beutenberg
Per term, one group of one or two students may work on the topic.
-
Wave Equation
Goals and context
- Basic concept of hyperbolic partial differential equations (PDEs) and the initial-boundary value problem (IVBP)
- Finite differencing methods for derivative approximation
- Method-of-line for time-domain PDEs with Runge-Kutta timesteps
- Numerical implementation of methods to solve multi-D PDEs
- Concepts of numerical stability and convergence
Methods
The students will solve the IBVP with the wave equation in 1+1 and 2+1 dimensions (one time dimension and one and two spatial dimensions) numerically. The project has different sequential steps:
- Wave equation and reduction to first order system
- Characteristic analysis and well-posedness
- Finite differencing approximation of derivatives and convergence
- Runge-Kutta time integrators
- Solution of IBVP withthe 1+1 wave equation and periodic boundaries using the method of lines
- Stability and convergence
- IBVP with open boundaries and Sommerfeld boundary conditions
- Wave equation with a potential: the Regge-Wheeler equation, scattering of graviational waves off a black hole and quasi-normal modes
- More spatial dimensions: the 2+1 wave equation
Students can code in their preferred language, although Python is strongly recommended (open sources, simple and optimal for visualizations).
Prerequisites
- Basic knowledge of partial differential equations
- Basic programming skills
Contact:
Person of charge: Prof. Dr. S. Bernuzzi
Supervision:
Place: Abbeanum, Fröbelstieg 1 or PAF Computerpool
Per term, one or two or three students may work on the topic.
Astronomy
-
Detection and Observation of Runaway Stars
Contents and learning objectives
Runaway stars are young, hot, massive or intermediate-mass stars showing a peculiarly high velocity with respect to the host cluster or OB association. They are moving away from their birth place, while the majority of others remain in their birth cluster. The high velocity nature of runaway stars is explained by two independent mechanisms:
- Dynamical ejection scenario (DES) proposes that the stars are ejected by gravitational interaction within the dense cores of the young clusters.
- Binary supernova scenario (BSS) brings an alternative explanation that the star is ejected by its orbital velocity due to the supernova of the binary companion.
Kinematic studies and observations of the young clusters has proven that the DES is working. On the other hand, high space velocities of isolated neutron stars imply that BSS is also viable. However, the star HD37424 is the only BSS runaway star which has been proven by observations. Finding BSS runaway stars provide us with great information on the supernova, supernova remnants (SNR) and neutron stars. The type of supernova, distance, age and all dependent parameters of the supernova remnant, the mass of the progenitor star and the kick given to the neutron star can be found. Therefore, exploring BSS runaways is now an important task in astrophysics. The BSS runaways can be found inside the supernova remnants (e.g. Spaghetti Nebula). The astrometry by the Gaia Satellite gives us precise distances and transverse motion vectors of the stars. A star having a significantly higher transverse velocity w.r.t the galactic neighborhood and moving away from an SNR is a potential candidate. These candidates can be detected through public astrometry and photometry data and be confirmed by spectroscopic observations. For bright stars (V<11 mag), the observations can be performed at the University Observatory in Grosschwabhausen. The project aims to teach students using astronomical catalogs, stellar kinematics, observations and data reduction and analysis.
Tasks
- Selection of stars within a certain position and distance range.
- Calculating the peculiar transverse velocity from proper motion of the stars
- Age estimates and tracing back the stellar motion in time
- Temperature and evolutionary stage estimation from photometry
- Analysis of archival stellar spectra
Contact:
Supervisor: Dr. Baha Dincel
Location (night observation): University Observatory in Großschwabhausen
Location (data reduction and analysis): Astrophysical Institute, Schillergäßchen 2, Jena
The tasks can be performed by one group with up to 2 students.
-
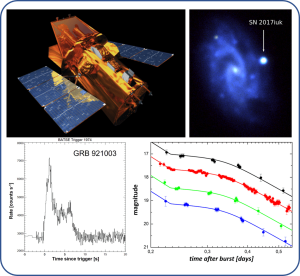
Gamma-Ray Burst Afterglows (not available in WS 25/26)
illustration of the Swift satellite (top left); host galaxy of GRB 171205A and associated GRB-SN 2017iuk (top right); light curve of GRB 921003 (bottom left); GRB-afterglow light curve of GRB 150413A (bottom right)
Foto: Sebastian SchmidlFrom the discovery of the first Gamma-Ray Burst (GRBs) in 1967, it took nearly 30 years to discover an optical transient related to a GRB, which allowed to place them at cosmologic distances. Since the 90's our knowledge of those cataclysmic events (emitted energy in gamma-rays: ~1051 - 1053 erg) has drastically expanded. We know today that these short-time gamma-ray sources (duration: a few 0.1 sec to several 100000 sec) can be found at redshifts z = 0.0085 to 9.4 (correlates to light travel time of 0.12 Gly to 13 Gly) and can be divided into two categories (long and short burst). Whereas long bursts (duration > 2 sec) are related to a special variant of type Ic supernova and short bursts (duration < 2 sec) are produced by the merger of two compact objects (preferably two neutron stars). The creation of the gamma-ray burst itself can be described within the fireball model by the collision of multiple shells traveling at high-relativistic velocities. After the burst, one can observe the afterglow of the GRB (from X-Ray to the Radio), which arises from the interaction of the shells and the interstellar material (ISM) and can be observed for several days to weeks.
The Project will focus on diffent aspects and caracteristics of the optical/NIR transients that follows the appearance of a GRB and the porperties of their host galaxies.
Tasks and Learning goals
- Reduction of photometric data in the VIS and NIR
- Analysis (photometry and astrometry) of photometric data
- Modeling of Afterglow light curves to derive the main properties of the transient(time and spectral evolution)
- search and modelling of Supernova components that can be found in the light curve
- investigating the properties of the GRB host galaxies (e.g. mass, age of the dominant stellar population, star formation rate)
- search within public archives for additonal data (data mining)
- deepening the understanding of relativistic outflows, Supernovae and the host galaxies of those events
- Observations at the TLS Tautenburg with the 2m Schmidt Telescope, if weather conditions are acceptable
Contact:
Supervision: Dr. habil Sylvio Klose; Dr. Sebastian Schmidl
Location: Thüringer Landessternwarte Tautenburg (TLS Tautenburg) and/or F-Pranktikum (please contact S. Schmidl for further informations)
Students can consider for example, to spend one day every two weeks in Tautenburg to work on the project.
-
Observation of Binary Stars
Contents and learning objectives
Since the discovery of the first binaries, visual, photometric and spectrometric observations have shown that most stars observable in the night sky are indeed stellar systems of two or even more stars. These binary or multiple star systems, which are bound together by their gravitational force, follow the laws of celestial mechanics, which were first empirically described by Kepler and then later astrophysically explained by Newton. Thanks to the classical mechanics, it is possible with observations to precisely determine the properties of the stars in these stellar systems, in particular their masses.
Since the mass of stars determines their evolution significantly, the observation and characterization of binary star systems is astrophysically very important. While wide binaries can still be observed directly with a telescope, more closer systems can be investigated spectroscopically by means of the Doppler effect. The movement of the components around their center of gravity reveals itself as a shift of the spectral lines in the common spectrum of the stellar system. The precise analysis of the radial velocities of the stars yields an exact characterization of the orbital parameters of the stellar system (e.g. period and orbital eccentricity) as well as its mass function or the mass ratio of its components.
In this project the students use the observing method described above for the detection and characterization of spectroscopic binary stars in order to determine the properties of these systems, as well as their actual orbital parameters. The students learn the important basics for the reduction and analysis of spectroscopic data of stars, which they themselves have taken with the modern instruments, operated at the University Observatory in Großschwabhausen.
Technology
The spectroscopic observations are carried out by the students at night at the University Observatory in Großschwabhausen (see Fig.2) with the Échelle spectrograph FLECHAS, which is operated at the 90cm reflector telescope of the observatory.
Supervisor: Dr. Markus Mugrauer
Location (night observation): University Observatory in Großschwabhausen
Location (data reduction and analysis): Astrophysical Institute, Schillergäßchen 2, Jena
Each spectroscopic binary system can be processed by 1 up to 3 students. The specific task will be adjusted depending on the observed stellar system.
-
Observation of Comets
Comets are small bodies in the Solar System consisting mainly of ice and dust. As well as comets on periodic orbits (the first of which was discovered by E. Halley), there are also many non-periodic comets. Recently, even interstellar comets have been discovered flying through the solar system. As comets spend most of their time far from the Sun, in the dark and cold depths of the solar system, they remain unobservable. However, as they approach the Sun, they begin to evaporate in the sunlight, forming a coma (the 'head' of the comet) and, eventually, a tail, which makes them visible in the night sky. As comets consist of almost unchanged, frozen matter from the early stages of the solar system, studying them provides important insights into the nature of matter during the formation process of the solar system. By observing comets, it is possible to determine their orbital elements and thus their place of origin in the solar system. Additionally, the activity of comets can be studied as they pass through the inner solar system.
Tasks:
- Observe new comets using the telescopes operated at the University Observatory in Großschwabhausen.
- Reduce and analyze all data, particularly with regard to astrometry (the position of the comets in sky), and photometry (the brightness of the comets).
- Examine the morphological evolution of the comets over time, such as coma diameter and tail length.
- Determine the orbital elements of the comets, as well as their absolute brightness dependant on the distance from the Sun.
- Study the activity of the comets dependant on solar distance, and search for non-gravitational forces that alter their orbits.
Technology
The imaging observations are carried out by the students at night at the University Observatory in Großschwabhausen with the CCD-cameras, which are operated at the individual telescopes of the observatory.
Contact:
Supervisor: Dr. Markus Mugrauer
Location (night observation): University Observatory in Großschwabhausen
Location (data reduction and analysis): Astrophysical Institute, Schillergäßchen 2, Jena
Each comet can be processed by 1 up to 3 students. The specific tasks will be adjusted depending on the observed comet.
-
Observation of Exoplanets
Contents and learning objectives
Since the discovery of the first planet outside our solar system some 20 years ago, more than 1000 of these exoplanets have been detected around distant stars. Several dozens of planets could be imaged directly next to their host star, using modern observing techniques on large telescopes of the 8 to 10m class. The vast majority of exoplanets, however, were detected indirectly by accurate spectrophoto-metric measurement of the light of their host stars. The transit method is today the most successfully used method for the planet search.
In the transit method, the occultation of the host star by its exoplanet is observed. By means of precise photometric measurements, the light curve of the star is measured during the transit of the planet, which allows the determination of the orbital period, the inclination of the planetary orbital plane and the planetary radius.
From the combination of the obtained results with available spectroscopic measurements (msin (i), minimum mass of the planet), the mean density of the exoplanet can be determined, which allows conclusions about its internal structure.
In this project, the students should use the observing method described above for the detection of planets in order to determine the properties of exoplanets, as well as their actual orbital parameters. The students learn the important basics for the reduction and analysis of photometric data of stars, which they themselves have recorded with the modern instruments, operated at the University Observatory in Großschwabhausen.
Technology
The photometric observations are carried out by the students at night at the University Observatory in Großschwabhausen (see Fig. 2) with the CCD-cameras, which are operated at the individual telescopes of the observatory.
Supervisor: Dr. Markus Mugrauer
Location (night observation): University Observatory in Großschwabhausen
Location (data reduction and analysis): Astrophysical Institute, Schillergäßchen 2, Jena
Each exoplanet can be processed by 1 up to 3 students. The specific task will be adjusted depending on the observed exoplanet.
-
Observation of Open Clusters
Contents and learning objectives
Stars are mostly born in open clusters and spend a significant part of their lives as a member of a cluster. An open cluster contains dozens or hundreds of stars formed at nearly the same time from the same nebula and loosely bound by mutual gravitational attraction. The cluster members share similar distance, age, metallicity, extinction, and velocity; hence they are the key objects in stellar evolution studies. Therefore, the differences in apparent brightness among members are due only to their intrinsic luminosities, thus their masses. The distances and the transverse velocities of the stars can be derived from the astrometric parallax and proper motion values respectively, measured by the Gaia Satellite. The color-magnitude (Hertzsprung–Russell) diagram of the cluster members indicates the age, metallicity and the extinction. The most massive and hottest stars of the cluster evolve faster, move away from the main sequence in the color-magnitude diagram and become cooler giants and/or supergiants. The position of the turn-off from the main sequence can be used to estimate the age of the cluster. To identify the properties of the members as well as the cluster variables, the color-magnitude diagram is fitted by a theoretical isochrone calculated for certain stellar evolution models and initial mass functions. However, the parameters determined by the isochrones must be tested by spectroscopic observations of the cluster members. The atmospheric parameters of the members derived from their spectra narrow down the uncertainty of theoretical isochrones.
This project aims to teach students how to determine the properties of the open clusters using astronomical catalogs, stellar evolution models, stellar kinematics, observations, data reduction and analysis.
Tasks
- Selection of cluster members regarding their positional and kinematic properties.
- Setting the color-magnitude diagram using optical and near-infrared photometry from various catalogs.
- Spectral observation, data reduction and analysis of the brightest members
- Measuring the effective temperature, surface gravity and metallicity of the stars
- Determination of the extinction and the cluster age by the isochrone fitting.
Contact:
Supervisor: Dr. Baha Dincel
Location (night observation): University Observatory in Großschwabhausen
Location (data reduction and analysis): Astrophysical Institute, Schillergäßchen 2, Jena
The tasks can be performed by up to 2 students.
-
Supernova Remnants
Supernova remnants (SNRs) are extended nebulae formed by the violent explosion of stars. Their optically visible emission comes mainly from shock-heated gas, producing bright filamentary structures in emission lines such as Halpha, [O III], and [S II] in their spectra . Optical studies of SNRs provide unique information on the shock physics, chemical abundances of the interstellar medium, and the dynamical evolution of the explosion debris. While X-ray and radio observations probe the high-energy plasma and relativistic particles, optical observations offer direct measurements of ionisation states, densities, and velocities. Narrow-band imaging allows us to map the morphology of the filaments, while spectroscopy provides line ratios to diagnose shock conditions, electron densities, and shock velocities.
This lab exercise focuses on the optical analysis of supernova remnants through both archival data and new observations. Students will learn how to process and analyse photometric and spectroscopic data of SNRs using IRAF and Python (Astropy, specutils, photutils). In addition to data reduction and interpretation, emphasis will be placed on conducting a lab project using public datasets and, when possible, telescope observations.
Tasks- Selection of a supernova remnant for study from available catalogs (e.g., Greens SNR catalog)
- Reduction and calibration of spectroscopic data and measurement of emission line fluxes and construction of diagnostic line ratio maps ([S II]/Halpha, [O III]/Hbeta)
- Extraction of physical parameters such as electron density, temperature, and shock velocity from spectra
- Photometric analysis of filamentary structures to estimate surface brightness and compare with models
- Doppler shift measurements of emission lines to obtain expansion velocities
Contact:
Supervisor: Günay Paylı-Bulut
The tasks can be worked on by up 1 or 2 students