Metronom-Spin stabilisiert zeitlich-kristalline Dynamik
Neues Paper von Niklas Euler und Adrian Braemer veröffentlicht
An illustration of the two-step Floquet cycle of the one-dimensional (1D) system considered in this work.
Meldung vom:
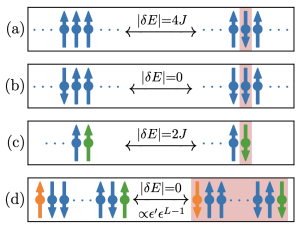
A visual summary of the different spin-flipping processes and their associated energy differences. The spins in the bulk are colored blue, whereas the metronome is colored orange, and the right edge spin is colored green. Flipped spins are highlighted with a red background.
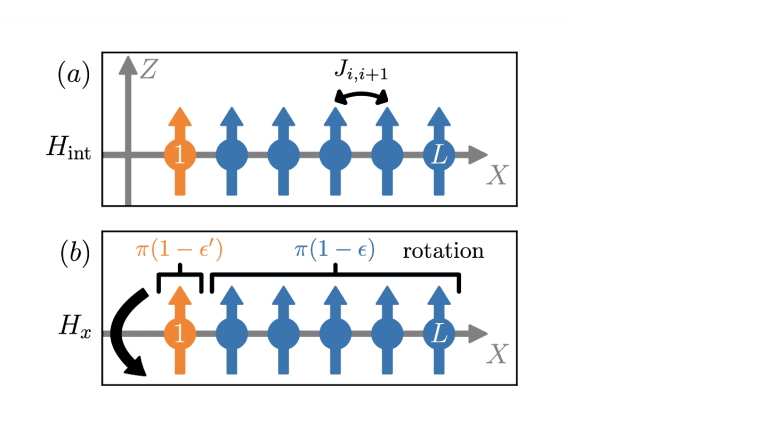
Foto: Niklas Euler, Adrian Braemer, Luca Benn, Martin GärttnerIm Paper wird eine ungeordnete Quanten-Ising-Kette, die einem zeitperiodischen Antrieb unterliegt, der jeden Spin um einen Winkel π(1-εi) dreht, untersucht. Wenn alle Spins die gleiche Abweichung ε erfahren und das System in einem vollständig polarisierten Zustand initialisiert wird, ist die Dynamik bekanntlich zeitkristallin: Die Magnetisierung des Systems zeigt periodisch verdoppelte Oszillationen für Zeitskalen, die exponentiell mit der Länge der Kette wachsen. In dieser Arbeit wird die Wirkung einer Abweichung ε, die zwischen den Spins unterschiedlich ist, untersucht. Es wird festgestellt, dass eine Verringerung von ε für einen einzelnen Spin die Lebensdauer der räumlich-zeitlichen Ordnung drastisch erhöht, was den Namen „Metronom“-Spin nahelegt. Mit Hilfe von Störungsargumenten in einem durchschnittlichen Hamilton-Bild wird diese Beobachtung für Ausgangszustände mit makroskopischer Massenmagnetisierung erklärt. Darüber hinaus wird, im Fall von zufälligen Bitstring-Anfangszuständen, über die Erhöhung der Lebensdauer einer topologischen Randmode, die ebenfalls in demselben Bild verstanden werden kann, berichtet. Schließlich wird eine veränderte Geometrie, bei der der Metronomspin nicht direkt Teil der Kette ist, was die Dynamik in den beiden betrachteten Szenarien auf unterschiedliche Weise beeinflusst, diskutiert. Unsere Ergebnisse enthüllen die komplizierte Dynamik, die in Floquet-Systemen unter dem Einfluss eines räumlich variierenden Antriebs auftritt, und eröffnen damit neue Wege für die Floquet-Technik.